Buscar un Patrón

-
Es una estrategia que se puede utilizar para buscar patrones en los datos con el fin de resolver problemas. La finalidad de dicha estrategia es buscar datos o números que se repiten.

Este día en la clase se aprendió sobre esta nueva técnica para la resolución de problemas, la cual consideramos que se debe de tomar en cuenta y aplicarlo en nuestro diario vivir, ya que nos puede ser útil. Esta estrategia consiste en lograr identificar un patrón en el problema, puede ser numérico o algébrico, y esto se puede identificar al momento que se encuentra alguna repetición y de esta manera se encontrará la solución.

Con mis compañeros de clase fue la estrategia que más pudimos emplear a la hora de la resolución de problemas, en algunos casos era muy fácil lograr identificar el patrón, pero en otros casos es necesario hacer varios cálculos antes para poder encontrar el patrón.

Los 4 pasos de Polya pueden llegar a ser pesados, pero es importante para poder entender de una mejor manera que es lo que se nos está planteando.

En este tema se puede distribuir en los siguientes:

1.     SUCESIONES GRÁFICAS

Para resolverlos, se sugieren estos pasos:

a) Observar el contenido de los 3 primeros cuadros de la secuencia

b) Determinar cuál es el cambio que se genera a través de ellos

c) Aplicar mentalmente ese cambio para generar el cuarto cuadro, luego

verificar su relación con la sucesión original

d) Analizar las 3 respuestas que se tienen como alternativas y elegir

aquella que concuerde con la idea generada en el paso anterior

 

2.     PATRONES NUMÉRICOS

En muchos ejercicios se puede aplicar el razonamiento inductivo

para determinar el siguiente número en la lista. Probablemente

sea necesario usar la calculadora para establecer correctamente

las relaciones entre uno y otro elemento de la secuencia.

 

Habiendo determinado la lógica de la secuencia, se debe aplicar

para encontrar el próximo elemento.

 

3.     DIFERENCIAS SUCESIVAS

Algunos ejercicios numéricos no pueden resolverse por simple

inspección, entonces se utiliza este método para determinar él

siguiente número en la secuencia.

 

Se denomina la diferencia sucesiva porque se calcula la diferencia (la

resta) entre las parejas de números, de forma sucesiva, hasta

encontrar un patrón.

 

4.     OTROS PATRONES NUMÉRICOS

Existen otro tipo de ejercicios, en los cuales la regularidad con que

se presentan los elementos cambia y de ellos tiene que inferirse

su regla de formación, son patrones recurrentes.

 

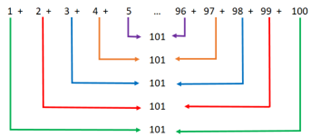
5.     MÉTODO DE GAUSS

Cuando Carl Friedrich Gauss (1777-1855) era muy joven, su profesor les pidió a

todos los alumnos que encontraran la suma de los primeros 100 números

naturales. Mientras sus compañeros se entretenían con los cálculos, él

simplemente, escribió un número y se le entregó a su maestro. ¡Y la respuesta

correcta!

 

El método de Gauss explica que entre 1 y 100, hay 50 pares de números cuya

suma es 101, por lo tanto, la suma de todos ellos debía ser 50 x 101 = 5050.





Comentarios

Publicar un comentario

Entradas populares de este blog

Conjunción y Disyunción

-
Imagen
Conjunción La conjunción es un conector lógico que se presenta cuando dos proposiciones arbitrarias se combinan mediante la palabra "y". Se denota P ʌ Q y se lee "P y Q". Valores de Verdad V - V = V V - F = F F - V = F F - F = F Podemos observar que solamente ese verdadero donde no se encuentre ninguna mezcla y tanto el antecedente como el consecuente sean verdaderos. Disyunción La disyunción se presenta cuando dos proposiciones arbitrarias se combinan mediante la palabra "o". Se denota P v Q y se lee "P o Q". Valores de Verdad V - V = V V - F = V F - V = V F - F = F En este caso se puede observar que al contrario de la conjunción en la disyunción solamente es falta cuando no contemos con ninguna mezcla y tanto el antecedente como el consecuente sean falsos.
Read more »

Diferencias Sucesivas

-
Imagen
Las diferencias sucesivas se utilizan para determinar el número siguiente de una sucesión, cuando a simple vista no se puede determinar. Es decir, si a primera vista la sucesión no resulta evidente, se debe emplear el método de las diferencias sucesivas para encontrar la siguiente sucesión. El método de las diferencias sucesivas consiste ene encontrar la diferencias de dos números sucesivos, es decir, la diferencias que hay en el segundo número y el primer número, la diferencias que hay entre el tercer número y segundo número y así sucesivamente, hasta llegar a un número constante en las diferencias. Ejemplo de una Diferencia Sucesiva Algunas secuencias presentan mayor dificultad para hacer una conjetura acerca del término que sigue. Con frecuencia se debe aplicar el método de diferencias sucesivas en estos casos. Considera la secuencia: 2,6,22,56,114... Como no es evidente cuál es el término que sigue, se resta el primer término del segundo, el segundo del tercero, el tercero del cua
Read more »

Hacer Diagrama o Figura

-
Imagen
Si te gusta dibujar o ser creativo para resolver los problemas, esta es una de las mejores estrategias para poder visualizar de una mejor forma el problema, como su nombre lo indica, dicha estrategia se basa en hacer figuras o diagramas para poder resolver problemas matemáticos. Muchos se preguntarán de qué forma el hacer una figura o algún diagrama nos puede favorecer en la resolución de los problemas, pues es la respuesta, esto es porque de esta manera tener una visualización de los que el problema nos pide, hace que tengamos mejores ideas de como es el problema al momento de plasmarlo el papel y así también mejores ideas de las posibles respuestas que podamos obtener de las conjeturas. Para realizar esto colocamos los datos del problema y los datos que se esperan obtener de este, en la figura o diagrama que suponemos nos pueda ayudar a comprender mejor el problema, en este tipo de estrategias lo que predomina es la creatividad y sobre todo a tomar nuevas perspectivas.
Read more »